大模型+强化学习_自我对弈偏好优化

英文名称: A Minimaximalist Approach to Reinforcement Learning from Human Feedback
中文名称: 一种极简极大化的强化学习方法：来自人类反馈的学习
链接: http://arxiv.org/abs/2401.04056v1
作者: Gokul Swamy, Christoph Dann, Rahul Kidambi, Zhiwei Steven Wu, Alekh Agarwal
机构: Google Research
日期: 2024-01-08

1 读后感

"Minimax Winner" 是博弈论中的一个概念，指的是在最坏情况下尽量最大化自己的收益。在这里将偏好学习视为一种零和博弈。

我觉得它的原理是这样的：大型模型是通过大量数据进行训练得到的生成模型，因此在生成结果时可能存在不稳定性，有时会表现出某些数据特征，而有时则表现出其他特征。有时候它可能会产生幻觉或相互矛盾的结果。

提出的方法相当于针对同一个问题生成多种答案，然后让模型选择最佳答案。选择过程实际上是让模型根据已有知识进行思考和推理，以反映大多数人的偏好，并选择更合逻辑，并使用获取到的数据对模型进行训练。

从论文内容来看，我很喜欢引言部分的开拓思路分析，但方法部分使用了过多符号表达，推理较难理解。不过结果并不复杂。

2 摘要

目标：提出一种基于模型自我对弈的强化学习算法。

方法：构建自我对弈偏好优化（SPO）算法，不需要训练奖励模型，也不需要不稳定的对抗训练，因此实施起来相当简单。通过单一代理自我对弈来计算最优策略，采样多条轨迹，让评价者比较并使用胜利比例作为奖励。

结论：在连续控制任务中，SPO 算法比基于奖励模型的方法学习更高效，同时对于实践中经常出现的不可传递和随机偏好具有鲁棒性。

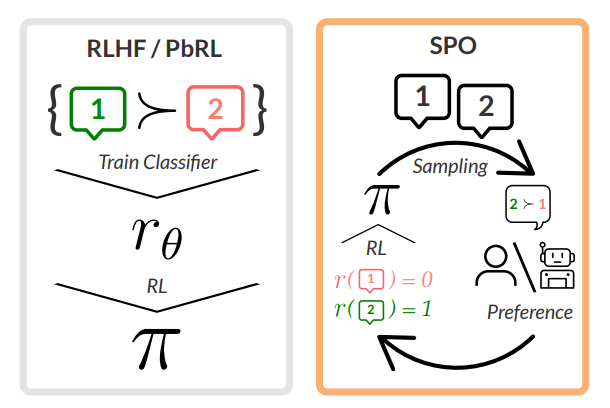
图 1：基于偏好的 RL/RLHF 的标准管道（左）涉及基于成对偏好数据集训练奖励模型，然后通过强化学习方法 RL 对优化模型策略 π。右图为文中 SPO 方法，它是一种迭代方法，直接根据评估者或偏好模型提供的偏好反馈进行优化，每个轨迹的奖励基于其相对于其他在策略轨迹的优先级比例来获得。通过经验证明和验证，这种方法比以前的工作更能适应不传递、非马尔可夫和嘈杂的偏好。

3 引言

RLHF 认为有潜在的奖励函数，就等价于假设存在一个总的顺序，A≻B,B≻C⇒A≻C（传递）。然而，心理学告诉我们实际人类决策的内容是相互矛盾的（石头剪刀布）。即使人们认为一个人的偏好是可传递的，但在评估者群体中，很难满足传递性。此外，如果两个选项得分相似，则选择任一条都不能满足中一半评估者。

作者提出了一种方法：从智能体中抽取多个轨迹，并要求评分者或偏好模型比较每对，并将奖励设置为轨迹的胜率。将这种方法称为 SPO。

4 方法

4.1 社会选择理论

图 3：一个简单的偏好函数 P1 在（a, b, c, d）上。如果 x ≻ y，那么 P1(x, y) = 1；如果 y ≻ x，那么 P1(x, y) = -1；如果 x ∼ y，那么 P1(x, y) = 0。

最自然的想法可能是选择击败最多其他选项的那个选项。在上述矩阵中，这可能是选项 a 或者 d，因为它们的行和最大。更正式地说，这种技术被称为 Copeland Winner。

推理链在此问题中不成立，a≻c，c≻d，d≻a，这就意思着有一半的判断者无法被满足。

5 方法

在每一轮中，算法会根据当前策略πt 生成一个轨迹ξt，然后计算这个轨迹相对于其他轨迹的胜率 rt(ξt)。这个胜率作为轨迹的奖励，用于更新策略。

5.1 相关概念

No-regret algorithm（无遗憾算法）：力求在长期运行中保持较小的累积损失。每一轮中，算法都会根据当前的信息和历史决策来选择一个动作（action），同时跟踪如果选择了其他动作可能获得的收益。
anti-symmetry（反对称性）：如果 a 和 b 是不同的元素，那么 a>b 和 b>a 不能同时为真。