用布林线的变种计算支撑位
1 引子
这是一个奇怪的脑洞:想到一种计算支撑位的量化方法。
早上和 AI 讨论如何识别阻力位和支撑位。它给我建议了几种方法,包括低点聚类、计算筹码密集区、斐波那契回调、均线以及最大回撤。这些方法与我对支撑的理解不太相符,而且都过于复杂,频繁处理多支股票数据比较耗费资源。
于是,我想到一个关于“平台”的逻辑。其中最简单的一种情况是:如果在某个区间震荡了一段时间后向上/向下突破,那么这个区间就可以作为支撑或阻力位。它应该是价格相对集中、波动较小的一段区间,具体可以通过中值和标准差来判断。
这是不是有点像布林带? 只不过布林带用的是均值和标准差。那么,是否可以通过稍作修改布林带的计算方法,简单地计算阻力和支撑位呢?
2 支撑位
在不同行情中,比如横盘震荡、上升趋势或下行趋势中,支撑位都是价格止跌反弹的位置。在上升趋势中,支撑位通常是向上通道的下轨或最近一轮上涨的低点;在下行趋势中,支撑位可能是历史低点或先前平台的下沿,尽管在下跌过程中较难判断底部。在横盘震荡时,支撑位出现在历史K线中多次试探并止跌反弹的位置。无论是哪种,都需要:多次回踩未破后反弹。
它的本质是买方意愿 + 成本密度 + 心理锚点的叠加。
| 市场类型 | 支撑识别逻辑 | 关键因子 |
|---|---|---|
| 横盘 | 波动率低 + 多次止跌区间 | 中位数、标准差 |
| 上升 | 趋势斜率>0 + 局部回撤低点 | 通道线、局部极小值 |
| 下行 | 趋势斜率<0 + 历史平台下沿 | 低点密集度、反弹验证 |
2.1 功能
- 如果不破位,趋势可能延续,可以将其视为买入点。
- 如果破位,趋势可能转弱或反转,可能是卖出的参考点。
所以有时候我们发现大模型给出的止损点和加仓点很接近,恰恰说明那一段价格区是“市场的临界点”。
3 布林线
布林线(Bollinger Bands)用于描述价格的相对波动区间。它涵盖了趋势、波动率和均值回归这三种市场特征。
3.1 计算方法
布林线由三条线组成:
- 中轨线(MB):通常是 N 日移动平均(MA)
- 上轨线(UB):MB + k × 标准差(σ)
- 下轨线(LB):MB − k × 标准差(σ)
一般参数为:N=20,k=2。
这三条线共同构成了一个随市场波动而自动调整的“通道”。
3.2 原理
简单来说,布林线就是将“均值+波动”可视化。它的原理是假设价格近似服从正态分布,表示价格波动的 95% 概率区间。也就是说,大部分价格波动都会落在上下轨之间。当波动率(标准差)增大时,通道会张开;当市场平静时,通道会收窄。
3.3 功能
- 波动率判断
- 通道收口 → 市场正在盘整,可能在酝酿趋势的爆发;
- 通道张口 → 市场剧烈波动,趋势可能延续或接近尾声。
- 趋势识别
- 价格沿上轨运行 → 强势趋势;
- 价格沿下轨运行 → 弱势趋势;
- 中轨(均线)常作为趋势中的支撑或阻力线。
- 买卖信号(均值回归思路)
- 当价格触及下轨并出现反弹信号 → 可能短期超跌;
- 当价格触及上轨并发生反转 → 可能短期超涨;
- 但若是强趋势行情,价格“贴轨”反而是趋势延续的信号。
4 中位数支撑模型
我早上想到的方法,暂时将它叫作“中位数支撑模型”。 核心想法是:用中位数代替布林带中均值,更稳当地识别价格的中枢区域。
4.1 原理
在设定的时间窗口(比如20天、60天)内: - 计算这段时间的中位数; - 再计算价格相对于中位数的波动范围,可用: - 标准差(Std) - 或更稳健的中位数绝对偏差(MAD); - 通过中位数 ± k × 波动度构建一个通道: - 下轨:中位数 − k × 波动度 → 支撑位; - 上轨:中位数 + k × 波动度 → 压力位或突破参考。
如果波动太大,说明价格还没收敛,不容易找到支撑;
如果波动较小,价格区间收紧,就可能在“构筑支撑”。
4.2 用法
- 当价格靠近下沿并止跌反弹 → 支撑有效;
- 当价格突破上沿、波动放大 → 可能是趋势启动;
- 如果下沿被明显跌破 → 支撑失效,趋势可能转弱。
4.3 示例
下图分别绘出了第20/40/60天对应的阻力位和支撑位(时间窗口为20天),其中蓝点因MAD过大(一直在上涨过程中,MAD超过中值的5%)而无法识别出阻力和支撑。
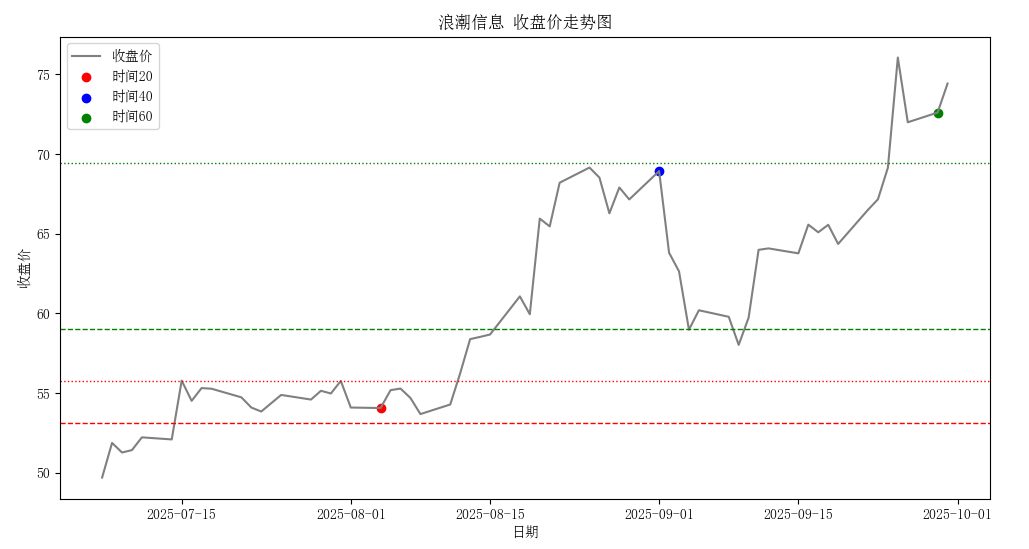
4.4 注意事项
- 时间窗口的选取很关键,不同周期信号差异会很大;
- 在强趋势行情里,中位数的反应会偏慢一点;
- 不是每个时间段都能算出“有效支撑”,波动太大的区间要单独处理。
5 布林线 vs 中位数支撑模型
| 维度 | 布林线(Bollinger Bands) | 中位数支撑模型 |
|---|---|---|
| 中心趋势 | 均值(Mean) | 中位数(Median) |
| 波动度指标 | 标准差(Std) | 标准差或中位绝对偏差(MAD) |
| 统计特性 | 对极值敏感 | 对极值鲁棒(稳健) |
| 市场假设 | 价格近似正态分布 | 价格分布未知但有集中性 |
| 主要用途 | 趋势识别 + 波动检测 | 平台识别 + 支撑判断 |
| 对强趋势反应 | 快速(容易“贴轨”) | 稳健但略有滞后 |
| 对震荡市场反应 | 易假突破 | 更能识别真实区间 |
