TFIDF与BM25
TFIDF
先复习一下 tfidf,tf 是词频,即某个词 i 在 文章 j 中出现的频率。分母是文章中所有词的个数,分母是词 i 出现的次数。tf 越高说明该词越重要,对于短文本匹配,每个词一般只出现一次,tf 的大小就取决于分母,即文章的长度。
\[ tf_{i,j}=\frac{n_{i,j}}{\sum_kn_{k,j}} \]
idf 是逆文档频率,计算该词出现在所有文章中的频率,此时,分母是包含该关键字 i 的文章数,分子是所有文章数 N。用 log 相当于趋势不变,数值变小了。该词出现越多,分子越大,idf 值越小,比如:" 的 " 经常出现,因此不是关键词。当词 i 在 文章 j 中完全不出现,分母为 0,因此给分母加 1。
\[ idf_i=log\frac{N}{df_i+1} \]
tf 和 idf 的乘积就是词 i 在文章 j 中的重要性。
\[ tfidf_{i,j}=tf_{i,j} \times idf_i \]
在搜索中,计算搜索串中的多个关键词 与 文章 j 的相似度:将各词的 tfidf 相加:
$$
similarity = {i} tfidf{i,j} $$
搜索之前,需要知道各个词在已知文章集中的分布。
BM25
BM25 是基于 TF-IDF 的改进算法,BM 是 Best Match 最佳匹配的缩写,25 指的是第 25 次算法迭代。
idf 部分只做了微调:
\[ idf_i=log\frac{N-df_i+0.5}{df_i+0.5} \]
其中分母部分从所有文章中减去了包含 i 的文章,0.5 用于平滑。
接下来,又对 tf 做了如下调整:
\[ tfscore= \frac {(k + 1) \times tf} { k \times (1 - b + b \times \frac{L_d}{L_{avg}}) + tf} \]
这里引入了超参数 k 和 b。
先看分母中的括号,Ld 是文章长度,Lavg 是所有文章的平均长度,当文章长度与平均长度一致时,括号里值为 1,相当于未乘系数;当文章比平均长度短时,括号里的值小于 1,分母越小,上式结果越大,也就是说文章越短,每一个词越重要,这也与直觉一致。另外,长度的影响与 b 有关,b 越大,影响越大,b 的取值在 0-1 之间,当 b 为 0 时,完全不考虑长度的影响,b 一般取值为 0.75。
k 用于标准化词频的范围,将 tf 值压缩到 0~k+1 之间,其函数曲线如下:
\[ tfscore = \frac{(k + 1) \times tf}{k + tf} \]
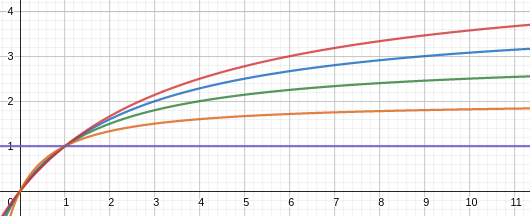
其横轴为 tf,纵轴为 tfscore,分别针对 k=0,1,2,3,4 画图。当 k=0 时,tfscore 为 1,不考虑词频的影响,而 k 越大词频越趋近于原始词频。因此,如果文章只包含短文本,或者无需关注词出现几次,则可将其设成 k=0。
有时还考虑到词 i 在搜索文本中的频率,上式扩展成:
\[ \sum_{t \in q} log[\frac{N-df_i+0.5}{df_i+0.5}] \times \frac{(k_1+1)tf_{td}}{k_1(1-b+b \times \frac{L_d}{L_{avg}})+tf_{td}} \times \frac{(k_2+1)tf_{tq}}{k_2+tf_{tq}} \]
其中 td 指被搜索文本,tq 指搜索文本。
另外,看了一些代码,发现这里的 tf 与 tfidf 中的 tf 不同,它不是词出现在文档中的次数除文档长度,而是词的出现次数,通过 k1 控制 tfscore 的范围,通过 Ld/Lavg 控制文档长度的影响。
这样我们就可以细化的控制 tf 的占比,以及文章长度的影响,以适应各种不同情况下的搜索和匹配任务。注意设置参数 k 和 b。
之前的 BM25 算法集成在 gensim 里,最新的版本没有了,如果想使用,可以从旧版本里抽出来。
代码参考:
https://github.com/RaRe-Technologies/gensim/blob/3.8.3/gensim/summarization/bm25.py
